解四类函数与导数题应注意的问题

1
作者姓名：叶培杰

2
单位：推荐全球最大网赌正规平台欢迎您

3
学科:高中数学

4
地址:漳平市江滨路412号

5
手机号码:13605928302

6
邮箱：yepeijie@126.com

解四类函数与导数题应注意的问题

叶培杰

（推荐全球最大网赌正规平台欢迎您，福建龙岩   364400）

摘要：函数与导数作为高考必考内容，选择题、填空题、解答题皆有出现，但以解答题为主，难度中等偏上，特别是解答题，难度较大，很多同学望而生畏，在平时解题过程中易忽略一些细节和技巧方法，造成对而不全或放弃解答，下面谨从五类题型分析归纳应注意的问题。

关键词：导数题   注意   问题

一、根据函数的单调性求参数的取值范围时应注意检验

例1. 若函数在内为减函数，求的取值范围。

解：

由题意知在内恒成立

所以在内恒成立

记

则时，

经检验时，符合题意

的取值范围为

小结：在已知函数是增函数（或减函数），求参数的取值范围时，应令（或恒成立，解出参数的取值范围，然后检验参数的取值能否使恒等于0，若恒等于0，则参数的这个值应舍去，若不恒为0，则由（或恒成立解出的参数的取值范围确定，下面举一个参数的值舍去的例子。

例2. 函数在上为单调递减函数，求的取值范围。【推荐国内安全的网赌网站】

解：依题意在上恒成立

得

在上恒成立

即解得

检验：是一个常数函数，舍去

综上可得的取值范围是

二、已知极值求参数时，应注意检验

例3. 已知函数在处取得极大值10，则的值为_________。

错解：函数的导数为

由在处取得极大值10

可得

即为

解得：

错解分析：由于为极值点的必要不充分条件，因此本题中由及求得的值后还要验证，所得结果是否满足为函数的极大值点，正确的解法如下：

解：函数的导数为

由在处取得极大值10可得

即为

解得：

当时

可得在处取得极小值10，与题意不符。

当时

可得在处取得极大值10

综上可得：满足题意

小结：为极值点的必要不充分条件。

三、注意函数图象的渐近线问题

例4. 已知函数，曲线上存在不同的两点，使得曲线在这两点处的切线都与轴垂直，则实数的取值范围是（    ）

A.        B.       C.        D.

解：因为曲线上存在不同的两点，使得曲线在这两点处的切线与轴垂直

所以有两个不同的解

即得有两个不同的解

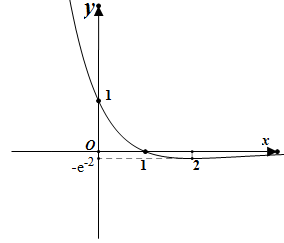设，则

所以时，

时，

所以时，函数取得极小值

图象如右图所示

由图可知，故选D

小结：因为当时，，所以当时，图象恒在轴下方，当时，图象在轴下方无限靠近轴，即轴是图象在时的渐近线，此题易忽视渐近线而错选C，所以解这类题目时应注意图象的渐近线问题，避免错解。

例5. （2014新课标全国Ⅰ）已知函数，若存在唯一的零点，且，则的取值范围是（    ）

A.         B.        C.         D.

解：由得

（若，则等式不成立）

令

令，得

当变化时，与的变化情况如下表

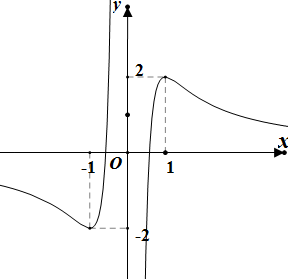图象如右图所示

依题意函数的图象与的图象有且只有一个交点，所以

小结：此题是我在上函数与方程这一节复习课与学生互动时，学生提供的一种思路即分离参数，研究两个函数图象的交点问题，但忽视了两条渐近线轴和轴，造成了有思路而错解的局面。

四、注意函数的定义域对解题的影响

例6. 若函数在其定义域的一个子区间内不是单调函数，则实数的取值范围是（    ）

A.        B.       C.         D.

解：  

函数在上单调递减，在上单调递增

得     

又

所以，故选D

分析：此题很多学生误选C，没有注意到是定义域的一个子区间，即，所以解函数题时应定义域优选原则，避免对而不全。

参考文献：

【推荐国内安全的网赌网站】叶培杰·对一类利用导数求参数取值范围问题解法的完善·福建中学数学2013（11）：46-47